第4单元　公钥密码

4.1　知识讲解

4.1.1　公钥密码的概念

传统对称密码体制要求通信双方使用相同的密钥，因此应用系统的安全性完全依赖于密钥的保密。

公钥密码体系，亦称非对称密码体系，加密和解密使用两把不同的密钥，加密算法和加密公钥可以公开，但是解密私钥必须保密，只有解密方知道。

公钥密码体系要求算法必须保证，任何攻击者都无法从公钥推算出私钥。

公钥密码体系中最著名的是RSA算法，此外还有背包密码、McEliece、Diffie-Hellman、Rabin、零知识证明、椭圆曲线、ElGamal算法等。

4.1.2　公钥密码的特点

明文(M)：作为算法输入的消息或数据。

加密(RSA)：对明文进行各种代换和变换。

密文(C)：作为算法输出，看似完全随机而杂乱的数据，依赖明文和秘钥：

• 对于给定的消息，不同的密钥产生不同的密文
• 密文是随机的数据流，其意义是无法被理解的

密钥(Key)：公钥(Public Key)和私钥(Private Key)成对出现，一个用来加密，另一个用来解密。

解密(RSA^-1)：接收密文，解密还原出明文。

公钥密码体系如下图所示：

4.1.3　RSA算法的原理

1. 生成公私密钥对

任选两个质数$p$和$q$ ，二者相乘得到$n$，即$n=p\times q$。如$p=3$，$q=11$，$n=3\times11=33$。

由欧拉函数$\phi(n)=(p-1)\times(q-1)$得到在$[1,n)$区间内与$n$互质的正整数个数。如$\phi(33)=(3-1)\times(11-1)=20$，即在$[1,33)$区间内有$1$、$2$、$4$、$\cdots$、$32$共$20$个正整数与$33$互质。

在$[1,\phi(n))$区间内选择一个与$\phi(n)$互质的正整数$e$，得到公钥$\{e,n\}$。如在$[1,20)$区间内选择与$20$互质的正整数$3$，得到公钥$\{3,33\}$。

确定正整数$d$，满足$d\times e\equiv1\%\phi(n)$，即方程$(d\times e-1)\%\phi(n)=0$的解，得到私钥$\{d,n\}$。如$(7\times3-1)\%20=0$，得到私钥$\{7,33\}$。式中符号“$\equiv$”表示同余，$a\equiv b\%c$表示$a$和$b$除以$c$所得余数相等。

2. 利用公钥$\{e,n\}$将明文分组$M$加密成密文分组$C$

$C=M^e\%n$

3. 利用私钥$\{d,n\}$将密文分组$C$解密成明文分组$M$

$M=C^d\%n$

4. 运算代价高，速度比对称加密慢几个数量级，不适合加密大量数据

用公钥加密私钥解密数字内容的对称密钥——防窃取、防监听。

用私钥加密公钥解密数字内容的消息摘要——防篡改、防抵赖。

4.2　实训案例

4.2.1　基于RSA算法的密钥分发

在第三单元“基于DES加密的TCP聊天”案例的基础上进行二次开发，利用RSA算法生成的非对称密钥加密和解密DES密钥。

在Linux平台上完成基于RSA算法加密通信程序的设计和实现。

程序包含DES密钥自动生成、RSA密钥分配和DES加密通信等三个部分。

程序实现全双工通信，并且加密过程对用户透明。

借助多路I/O或异步I/O技术，对网络通信功能的实现进行优化。

4.2.2　程序清单

1. 声明Rsa类

// rsa.h
// 声明Rsa类

#pragma once

#include <stdint.h>

// 基于RSA算法的加解密
class Rsa {
public:
    // 公钥
    typedef struct tag_PublicKey {
        uint64_t e, n;
    }   PUBKEY;

    // 私钥
    typedef struct tag_PrivateKey {
        uint64_t d, n;
    }   PRIKEY;

    // 生成公私密钥对
    void generateKey(PUBKEY& pubKey, PRIKEY& priKey) const;

    // 加密
    int encrypt(PUBKEY pubKey, const void* mbuf, size_t mlen,
        void* cbuf, size_t* clen) const;
    // 解密
    int decrypt(PRIKEY priKey, const void* cbuf, size_t clen,
        void* mbuf, size_t* mlen) const;

private:
    // 乘模运算：(axb)%c
    uint64_t mulMod(uint64_t a, uint64_t b, uint64_t c) const;
    // 幂模运算：(a^b)%c
    uint64_t powMod(uint64_t a, uint64_t b, uint64_t c) const;

    // 质数检测
    bool isPrime(uint64_t n) const;
    // 产生随机质数
    uint64_t randPrime(uint8_t bits) const;

    // 求最大公约数
    uint64_t gcd(uint64_t p, uint64_t q) const;
    // 求满足d×e≡1%ϕ(n)，即方程(d×e−1)%ϕ(n)=0的整数解d
    uint64_t euclid(uint64_t e, uint64_t fai_n) const;

    // 加密分组
    uint64_t M2C(PUBKEY pubKey, uint8_t M) const;
    // 解密分组
    uint8_t C2M(PRIKEY priKey, uint64_t C) const;

    // 随机数
    class Random {
    public:
        // 构造函数
        Random(unsigned int seed = 0);

        // 产生[a, b)区间内的随机数
        uint64_t number(uint64_t b, uint64_t a = 0) const;
    };

    Random random;
};

2. 实现Rsa类

// rsa.cpp
// 实现Rsa类

#include <math.h>
#include <time.h>
#include <stdlib.h>
#include <string.h>
#include <algorithm>
using namespace std;

#include "rsa.h"

// 生成公私密钥对
void Rsa::generateKey(PUBKEY& pubKey, PRIKEY& priKey) const {
    // 任意选取两个质数p和q
    uint64_t p = randPrime(16), q = randPrime(16);
    // 二者相乘得到n，即n=p×q
    uint64_t n = p * q;
    // 由欧拉函数ϕ(n)=(p−1)×(q−1)得到在[1,n)区间内与n互质的正整数个数
    uint64_t fai_n = (p - 1) * (q - 1);

    // 在[1,ϕ(n))区间内选择一个与ϕ(n)互质的正整数e
    uint64_t e;
    while (gcd(e = random.number(fai_n, 1), fai_n) != 1);
    // 得到公钥{e,n}
    pubKey.e = e;
    pubKey.n = n;

    // 确定正整数d，满足d×e≡1%ϕ(n)，即方程(d×e−1)%ϕ(n)=0的解
    uint64_t d = euclid(e, fai_n);
    // 得到私钥{d,n}
    priKey.d = d;
    priKey.n = n;
}

// 加密
int Rsa::encrypt(PUBKEY pubKey, const void* mbuf, size_t mlen,
    void* cbuf, size_t* clen) const {
    // 检查密文缓冲区长度
    size_t nlen = mlen * 8;
    if (*clen < nlen) {
        *clen = nlen;
        return -1;
    }

    *clen = nlen;

    const uint8_t* M = (const uint8_t*)mbuf;
    uint64_t* C = (uint64_t*)cbuf;

    while (mlen) {
        // 加密分组
        *C = M2C(pubKey, *M);

        ++C;
        ++M;
        --mlen;
    }

    return 0;
}

// 解密
int Rsa::decrypt(PRIKEY priKey, const void* cbuf, size_t clen,
    void* mbuf, size_t* mlen) const {
    // 检查明文缓冲区长度
    size_t nlen = clen / 8;
    if (*mlen < nlen) {
        *mlen = nlen;
        return -1;
    }

    *mlen = nlen;

    const uint64_t* C = (const uint64_t*)cbuf;
    uint8_t* M = (uint8_t*)mbuf;

    while (clen) {
        // 解密分组
        *M = C2M(priKey, *C);

        ++M;
        ++C;
        clen -= 8;
    }

    return 0;
}

// 乘模运算：(axb)%c
uint64_t Rsa::mulMod(uint64_t a, uint64_t b, uint64_t c) const {
    // (aXb)%c=(a%c)x(b%c)%c
    return (a % c) * (b % c) % c;
}

// 幂模运算：(a^b)%c
uint64_t Rsa::powMod(uint64_t a, uint64_t b, uint64_t c) const {
    // b=11(1011B)->(a^11)%c
    uint64_t d = 1, e = a % c, f = 1;
    /*
       +---+------------------+------------+-----+----------+
       | i |        e         |     f      | b&f |    d     |
       +---+------------------+------------+-----+----------+
       | 0 | (a^1)%c->(a^2)%c | 0001->0010 |  1  | (a^ 1)%c |
       | 1 | (a^2)%c->(a^4)%c | 0010->0100 |  1  | (a^ 3)%c |
       | 2 | (a^4)%c->(a^8)%c | 0100->1000 |  0  |          |
       | 3 | (a^8)%c->...     | 1000->...  |  1  | (a^11)%c |
       +---+------------------+------------+-----+----------+
    */
    for (int i = 0; i < 64; ++i) {
        if (b & f)
            d = mulMod(d, e, c);

        e = mulMod(e, e, c);
        f <<= 1;
    }

    return d;
}

// 质数检测
bool Rsa::isPrime(uint64_t n) const {
    for (uint64_t m = sqrtl(n); m > 1; --m)
        if (n % m == 0)
            return false;

    return true;
}

// 产生随机质数
uint64_t Rsa::randPrime(uint8_t bits) const {
    uint64_t numb = 1;
    numb <<= bits - 1; // 最高位是1，足够大
    numb += random.number(numb);
    numb |= 1; // 最低位是1，偶数不可能是质数

    if (! isPrime(numb))
        return randPrime(bits);

    return numb;
}

// 求最大公约数
uint64_t Rsa::gcd(uint64_t p, uint64_t q) const {
    if (p == q)
        return p;

    uint64_t a = max(p, q), b = min(p, q);
    while (b) { // 辗转相除法
        a %= b;
        swap(a, b);
    }

    return a;
}

// 求满足d×e≡1%ϕ(n)，即方程(d×e−1)%ϕ(n)=0的整数解
uint64_t Rsa::euclid(uint64_t e, uint64_t fai_n) const {
    // (d×e−1)%ϕ(n)=0
    // (d×e−1)/ϕ(n)=q
    // d=(qxϕ(n)+1)/e
    uint64_t max = (UINT64_MAX - 1) / fai_n;

    for(uint64_t q = 1; q <= max; ++q)
        if ((q * fai_n + 1) % e == 0)
            return (q * fai_n + 1) / e;

    return 0;
}

// 加密分组
uint64_t Rsa::M2C(PUBKEY pubKey, uint8_t M) const {
    // C=(M^e)%n
    return powMod(M, pubKey.e, pubKey.n);
}

// 解密分组
uint8_t Rsa::C2M(PRIKEY priKey, uint64_t C) const {
    // M=(C^d)%n
    return powMod(C, priKey.d, priKey.n);
}

////////////////////////////////////////////////////////////////////////

// 构造函数
Rsa::Random::Random(unsigned int seed /* = 0 */) {
    srand(seed ? seed : time (NULL));
}

// 产生[a, b)区间内的随机数
uint64_t Rsa::Random::number(uint64_t b, uint64_t a /* = 0 */) const {
    uint64_t r;
    uint32_t* rr = (uint32_t*)&r;

    rr[0] = rand();
    rr[1] = rand();

    return r % (b - a) + a;
}

3. 测试Rsa类

// rsa_test.cpp
// 测试Rsa类

#include <stdlib.h>
#include <string.h>
#include <iostream>
#include <iomanip>
#include <fstream>
using namespace std;

#include "rsa.h"

int main(void) {
    // 生成公私密钥对
    Rsa rsa;
    Rsa::PUBKEY pubKey;
    Rsa::PRIKEY priKey;
    rsa.generateKey(pubKey, priKey);
    cout << pubKey.e << ' ' << pubKey.n << endl;
    cout << priKey.d << ' ' << priKey.n << endl;

    // 保存公私密钥文件
    ofstream("./pubkey.dat", ios::binary).write((char*)&pubKey, sizeof(pubKey));
    ofstream("./prikey.dat", ios::binary).write((char*)&priKey, sizeof(pubKey));

    // 明文和密文缓冲区
    char mbuf[1024] = "Give back to Ceasar what is "
        "Ceasar's and to God what is God's";
    uint8_t cbuf[1024];
    size_t mlen = strlen(mbuf), clen;

    // 密文缓冲不足
    clen = 8;
    cout << rsa.encrypt(pubKey, mbuf, mlen, cbuf, &clen) << endl;
    cout << clen << endl;
    // 密文缓冲充足
    cout << rsa.encrypt(pubKey, mbuf, mlen, cbuf, &clen) << endl;
    // 打印十六进制密文
    cout << hex << setfill('0');
    for (size_t i = 0; i < clen; ++i)
        cout << setw(2) << (unsigned int)cbuf[i];
    cout << endl;

    // 明文缓冲区不足
    mlen = 8;
    cout << dec << rsa.decrypt(priKey, cbuf, clen, mbuf, &mlen) << endl;
    cout << mlen << endl;
    // 明文缓冲区充足
    cout << rsa.decrypt(priKey, cbuf, clen, mbuf, &mlen) << endl;
    cout << mlen << endl;
    mbuf[mlen] = '\0';
    cout << mbuf << endl; // 打印明文字符串

    return EXIT_SUCCESS;
}

4. 测试Rsa类构建脚本

# rsa_test.mak
# 测试Rsa类构建脚本

PROJ   = rsa_test
OBJS   = rsa_test.o rsa.o
CXX    = g++
LINK   = g++
RM     = rm -rf
CFLAGS = -c -g -Wall -I.

$(PROJ): $(OBJS)
    $(LINK) $^ -o $@

.cpp.o:
    $(CXX) $(CFLAGS) $^

clean:
    $(RM) $(PROJ) $(OBJS)

5. 声明MoreSecChat类

// moresecchat.h
// 声明MoreSecChat类

#include "secchat.h"
#include "rsa.h"

// 更安全聊天
class MoreSecChat : public SecChat {
public:
    // 构造函数
    MoreSecChat(const char* kfn, const char* port, const char* ip = "");

    // 聊天
    int chat(void) const;

private:
    // 生成并发送密钥
    virtual int sendKey(void);
    // 接收并保存密钥
    virtual int recvKey(void);

    string    kfn; // 公(私)密钥文件名
    const Rsa rsa; // 基于RSA算法的加解密
};

6. 实现MoreSecChat类

// moresecchat.cpp
// 实现MoreSecChat类

#include <unistd.h>
#include <sys/socket.h>
#include <iostream>
#include <fstream>
using namespace std;

#include "moresecchat.h"

// 构造函数
MoreSecChat::MoreSecChat(const char* kfn, const char* port,
    const char* ip /* = "" */) : SecChat(port, ip), kfn(kfn) {}

// 聊天
int MoreSecChat::chat(void) const {
    fd_set readfds;
    int nfds = max(STDIN_FILENO, sockfd) + 1;

    for (;;) {
        FD_ZERO(&readfds);
        FD_SET(STDIN_FILENO, &readfds);
        FD_SET(sockfd, &readfds);

        // 同时监视标准输入和套接字
        if (select(nfds, &readfds, NULL, NULL, NULL) == -1) {
            perror("select");
            close(sockfd);
            return -1;
        }

        // 若标准输入可读...
        if (FD_ISSET(STDIN_FILENO, &readfds))
            // 从标准输入读取字符串发送给对方主机
            if (send() == -1) {
                close(sockfd);
                return -1;
            }

        // 若套接字可读...
        if (FD_ISSET(sockfd, &readfds))
            // 从对方主机接收字符串打印到标准输出
            if (recv() == -1) {
                close(sockfd);
                return -1;
            }
    }

    return 0;
}

// 生成并发送密钥
int MoreSecChat::sendKey(void) {
    // 生成密钥
    key = des.generateKey();

    // 打开公钥文件
    ifstream ifs(kfn.c_str(), ios::binary);
    if (! ifs) {
        cerr << "Unable to open public key file" << endl;
        return -1;
    }

    // 读取公钥文件
    Rsa::PUBKEY pubKey;
    if (! ifs.read((char*)&pubKey, sizeof(pubKey)) ||
        ifs.gcount() != sizeof(pubKey)) {
        cerr << "Unable to read public key file" << endl;
        ifs.close();
        return -1;
    }

    ifs.close();

    // 用公钥加密密钥
    uint8_t ckey[64];
    size_t clen = sizeof(ckey);
    if (rsa.encrypt(pubKey, &key, sizeof(key), ckey, &clen) == -1) {
        cerr << "Unable to encrypt key" << endl;
        return -1;
    }

    // 发送密钥
    if (::send(sockfd, &ckey, clen, 0) != (ssize_t)clen) {
        perror("send");
        return -1;
    }

    return 0;
}

// 接收并保存密钥
int MoreSecChat::recvKey(void) {
    // 接收密钥
    uint8_t ckey[64];
    ssize_t clen = ::recv(sockfd, ckey, sizeof(ckey), 0);

    if (clen == -1) {
        perror("recv");
        return -1;
    }

    if (! clen) {
        cerr << "recv: " << "Connection break" << endl;
        return -1;
    }

    // 打开私钥文件
    ifstream ifs(kfn.c_str(), ios::binary);
    if (! ifs) {
        cerr << "Unable to open private key file" << endl;
        return -1;
    }

    // 读取私钥文件
    Rsa::PRIKEY priKey;
    if (! ifs.read((char*)&priKey, sizeof(priKey)) ||
        ifs.gcount() != sizeof(priKey)) {
        cerr << "Unable to read private key file" << endl;
        ifs.close();
        return -1;
    }

    ifs.close();

    // 用私钥解密密钥
    size_t mlen = sizeof(key);
    if (rsa.decrypt(priKey, ckey, clen, &key, &mlen) == -1) {
        cerr << "Unable to decrypt key" << endl;
        return -1;
    }

    return 0;
}

7. 测试MoreSecChat类

// moresecchat_test.cpp
// 测试MoreSecChat类

#include <stdlib.h>
#include <string.h>
#include <iostream>
using namespace std;

#include "moresecchat.h"

int main(int argc, char* argv[]) {
    if (argc < 3) // 检查命令行参数个数
        goto escape;

    if (! strcmp(argv[1], "-s")) { // 服务器
        // 更安全聊天服务器
        MoreSecChat server("./pubkey.dat", argv[2]);

        // 在侦听套接字上等待并接受对方主机的连接请求
        if (server.accept() == -1)
            return EXIT_FAILURE;

        // 聊天
        if (server.chat() == -1)
            return EXIT_FAILURE;
    }
    else if (! strcmp(argv[1], "-c")) { // 客户机
        if (argc < 4) // 检查命令行参数个数
            goto escape;

        // 更安全聊天客户机
        MoreSecChat client("./prikey.dat", argv[3], argv[2]);

        // 向对方主机发起连接请求
        if (client.connect() == -1)
            return EXIT_FAILURE;

        // 聊天
        if (client.chat() == -1)
            return EXIT_FAILURE;
    }
    else
        goto escape;

    // 返回成功
    return EXIT_SUCCESS;

escape:
    // 打印命令行帮助信息并返回失败
    cerr << "Usage: " << argv[0] << " -s <port>" << endl;
    cerr << "Usage: " << argv[0] << " -c <ip> <port>" << endl;
    return EXIT_FAILURE;
}

8. 测试MoreSecChat类构建脚本

# moresecchat_test.mak
# 测试MoreSecChat类构建脚本

PROJ   = moresecchat_test
OBJS   = moresecchat_test.o moresecchat.o secchat.o des.o rsa.o
CXX    = g++
LINK   = g++
RM     = rm -rf
CFLAGS = -c -g -Wall -I.

$(PROJ): $(OBJS)
    $(LINK) $^ -o $@

.cpp.o:
    $(CXX) $(CFLAGS) $^

clean:
    $(RM) $(PROJ) $(OBJS)

4.3　扩展提高

4.3.1　RSA算法的安全性

1. 目前针对RSA算法的攻击主要还是利用质因子分解法

RSA算法的公钥$\{e,n\}$是公开的，将其中的$n$分解为两个质数$p$和$q$的乘积，即$n=p\times q$。

根据$n$的两个质因子$p$和$q$计算出其欧拉函数$\phi(n)$的值，即$\phi(n)=(p-1)\times(q-1)$。

由已知的$e$求出满足方程$(d\times e-1)\%\phi(n)=0$的$d$，即得到私钥$\{d,n\}$，完成破解。

2. RSA算法的安全性依赖于对𝑛的质因子分解

当$n$足够大(如1024或2048个二进制位)时，迄今尚无任何计算工具可以从中分解出$p$和$q$因子。

3. 目前从理论上还无法证明，大数分解是破解RSA算法的唯一途径

RSA算法的安全性是否与大数分解的难度完全等价，缺乏理论上的支持。

但从近30年的历史来看，RSA算法经受住了各种攻击的考验，其安全性已被事实所证明。

4.3.2　其它公钥密码

椭圆曲线密码学(Elliptic Curve Cryptography，ECC)是基于椭圆曲线数学的一种公钥密码算法。

1. 椭圆曲线

这里的椭圆曲线并非圆锥曲线意义上的椭圆曲线：

$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\quad(a>b>0)$

而是源自用于计算椭圆周长的椭圆积分：

$\int_{c}^{x}R[t,\sqrt{P(t)}]dt$

其中$R$是其两个参数的有理函数，$P$是一个无重根的3或4阶多项式，而$c$是一个常数。椭圆曲线方程与$P$的表现形式比较相像。数学上的椭圆曲线是指由维尔斯特拉斯(Weierstrass)方程所确定的平面曲线，其一般形式为：

$y^2=x^3+ax^2+bx+c$

其中

$\Delta(E)=-4a^3c+a^2b^2-4b^3-27c^2+18abc\ne0$

典型的椭圆曲线，如$y^2=x^3-4x^2+16$，其函数图像如下所示：

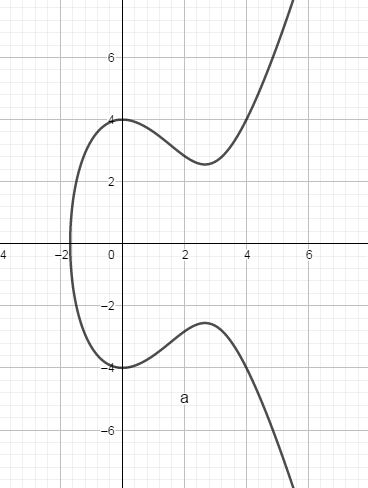
在密码学中使用的椭圆曲线方程一般被限定为：

$y^2=x^3+ax+b$

即二次项系数为0，其中

$\Delta(E)=4a^3+27b^2\ne0$

2. 椭圆曲线算术

1) 加法

已知椭圆曲线上两个不同的点$P$和$Q$，它们的和$R=P+Q$，可依如下方法得到：

• 过$P$、$Q$两点做直线$L$，与椭圆曲线相交于$R'$点
• $R'$点关于$X$轴的对称点即为$P$、$Q$两点之和$R$点
• 椭圆曲线关于$X$轴对称，故$R$点亦在椭圆曲线上

如下图所示：

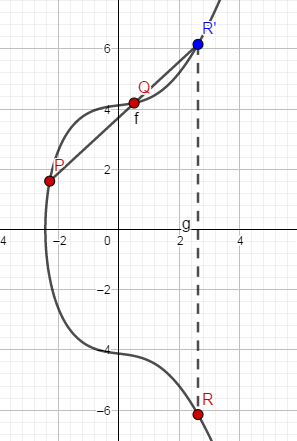
另外，$-P$点是$P$点关于$X$轴的对称点，亦在椭圆曲线上。

2) 数乘

移动$Q$点至与$P$点重合，直线$L$即成为椭圆曲线上过$P$点的切线，此时的$R$点为$P$点与$P$点之和，即$R=P+P=2P$，依此类推可以得到$3P$、$4P$、……，直至$kP\,(k\ge1)$，此即椭圆曲线的数乘。

3. 椭圆曲线的离散对数问题

假设数$k$和$P$点已知，可以很容易地计算其数乘的结果$Q=kP$，但反过来在已知$P$点和$Q$点的前提下，计算数$k$却相当困难，此即椭圆曲线的离散对数问题。

正因为如此，可以将$Q$作为公钥，公开出去，$k$作为私钥，秘密保管，通过公钥破解私钥将十分困难。

4. 基于椭圆曲线的加解密

应用于密码体系中的椭圆曲线都是定义在有限域上的，即：

$y^2\equiv(x^3+ax+b)\%p$

其中$p$称为模数。

1) 生成公私密钥对

在椭圆曲线$y^2\equiv(x^3-4)\%199$上选取$P=(2,2)$和数$k=119$，计算$Q=kP=119(2,2)=(183,173)$，得到：

• 公钥：$Q=(183,173)$
• 私钥：$k=119$

2) 加密运算

将明文$76$代入椭圆曲线方程$y^2\equiv(x^3-4)\%199$，得到明文点：

$M=(76,66)$

随机选取一个正整数$n=133$，利用公钥依下式根据明文点计算密文点：

$\begin{aligned} C&=\{C_1,C_2\} \\ &=\{nP,M+nQ\} \\ &=\{133(2,2),(76,66)+133(183,173)\} \\ &=\{(40,147),(180,163)\} \end{aligned}$

3) 解密运算

利用私钥依下式根据密文点计算明文点：

$\begin{aligned} M&=C_2-kC_1 \\ &=(180,163)-119(40,147) \\ &=(180,163)-(98,52) \\ &=(76,66) \end{aligned}$

5. 椭圆曲线密码体系的安全性

椭圆曲线密码体系是截至目前每比特加密强度最高的一种公钥密码体系。破解椭圆曲线密钥的时间复杂度是指数级($O(2^N)$)的，远高于子指数级时间复杂度的RSA算法：

• 有研究表明160位椭圆曲线密钥的安全强度与1024位RSA密钥相当
• 在每秒执行一百万条指令的处理器上，破解234位椭圆曲线密钥，需要1.6x10²⁸年

我国国家标准对各种加密算法的最小密钥长度做了如下规定：

• 对称分组加密：80位
• RSA加密：1024位
• 椭圆曲线加密：160位

4.3.3　多路I/O

为了提高程序的运行效率，Linux系统提供了select函数。借助该函数，调用者可在一个线程中同时监视多个文件描述符上的I/O事件，哪个文件描述符读/写就绪了就读/写哪个文件描述符，而不必为每个可能发生阻塞的文件描述符开辟单独的进程或者线程。如下图所示：

select函数的原型如下所示：

#include <sys/select.h>

int select(
    int              nfds,      // 被监视文件描述符中的最大值加一
    fd_set         * readfds,   // 监视这些文件描述符上的可读事件
    fd_set         * writefds,  // 监视这些文件描述符上的可写事件
    fd_set         * exceptfds, // 监视这些文件描述符上的异常事件
    struct timeval * timeout    // 在此时间内未发生任何事件则返回
);

该函数成功返回有事件发生的文件描述符总数，或者0如果超时，失败返回-1，同时设置errno变量。

用于操作文件描述符集的四个便捷宏：

void FD_CLR   (int fd, fd_set * set); // 清除文件描述符集中的特定文件描述符
int  FD_ISSET (int fd, fd_set * set); // 特定文件描述符是否在文件描述符集中
void FD_SET   (int fd, fd_set * set); // 将特定文件描述符加入文件描述符集中
void FD_ZERO  (        fd_set * set); // 清除文件描述符集中的全部文件描述符

表示超时时间的结构：

#include <sys/time.h>

struct timeval {
    long tv_sec;  // 秒
    long tv_usec; // 微秒(1/1000000秒)
};

调用select函数时将timeout参数指定为NULL，表示无限期等待事件发生。

达内集团◇C++教研部◇闵卫